[1] 실험값
(1) 실험 1 – [2] 회전 장치의 기본 틀(회전축+3단 도르래+알루미늄 트랙)의 관성모멘트 측정
-3단 도르래의 반지름 r
-상단 도르래: r = 0.85cm
-중단 도르래: r = 1.25cm
-하단 도르래: r = 2.975cm
-추걸이와 추를 합한 질량 m=55g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm
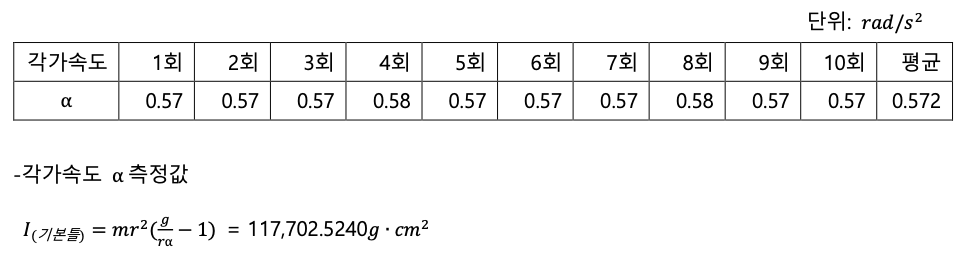
(2) 실험 2–[3] 질점으로 간주할 수 있는 사각추의 관성모멘트 측정
-사각추의 질량 M = 278.55g
1 사각추의 회전 반지름 R=0cm
-𝐼(이론사각추) = 𝑀𝑅^2 = 0𝑔 ∙ 𝑐𝑚^2
-추걸이와 추를 합한 질량 m=55g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm
-각가속도 α측정값

2 사각추의 회전 반지름 R=5cm
-𝐼(이론사각추) = 𝑀𝑅! = 6,963.75𝑔 ∙ 𝑐𝑚!
-추걸이와 추를 합한 질량 m=55g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm
-각가속도 α측정값

3 사각추의 회전 반지름 R = 10 m
-𝐼(이론사각추) = 𝑀𝑅^2 = 278.55𝑔 ∙ 𝑐𝑚^2
-추걸이와 추를 합한 질량 m=55g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm
-각가속도 α측정값

4 사각추의 회전 반지름 R = 20cm
-𝐼(이론사각추) = 𝑀𝑅^2 = 111,420𝑔 ∙ 𝑐𝑚^2
-추걸이와 추를 합한 질량 m=55g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm
-각가속도 α측정값

5 사각추의 질량 M=560.09g, 사각추의 회전 반지름 R=5cm
-𝐼(이론사각추) = 𝑀𝑅! = 14,002.25𝑔 ∙ 𝑐𝑚^2
-추걸이와 추를 합한 질량 m=55g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm
-각가속도 α측정값

(3) 실험 3–[4]1차원 강체로 간주할 수 있는 막대의 관성모멘트 측정 -막대의 질량 M = 628.5g
-막대의 길이 L = 40cm
1 막대의 중심을 지나는 축에 대한 관성모멘트 측정
-𝐼(이론막대, cm) = 0 𝑀𝐿! = 83,800𝑔 ∙ 𝑐𝑚^2
-추걸이와 추를 합한 질량 m = 104.47g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm

2 막대의 중심을 지나는 축에 대한 관성모멘트 측정
-𝐼(이론막대, cm) = 0 𝑀𝐿! = 335,200𝑔 ∙ 𝑐𝑚^2
-추걸이와 추를 합한 질량 m = 104.47g
-3단 도르래 중 실을 감은 도르래의 반지름 r=1.25cm

[2] 결과 분석

실험 2의 1, 2, 3, 4에서는 사각추의 질량 M을 286.55g으로 고정하고 사각추의 회전 반지름 R 을 0cm, 5cm, 10cm, 15cm 로 5cm 씩 변화시키며 실험을 진행하였다. 사각추의 질량을 고정하고 회전 반지름을 변화시키면서 실험 2-1 각가속도 평균은 0.562, 표준편차는 0.004 실험 2-2 각가속도 평균은 0.53, 표준편차는 0.00447 실험-3 각가속도 평균은 0.45, 표준편차는 0.00632 실험-4 각가속도 평균은 0.286, 표준편차는 0.00663(모든 단위는 𝑟𝑎𝑑/𝑠!)으로 평균이 점점 줄어드는 것을 확인할 수 있다. 상당히 작은 표준편차들을 통해 우리 실험은 신뢰성이 높으며, 각각의 평균값들을 통해 사각추의 회전 반지름이 증가할수록 각가속도가 감소함을 확인할 수 있다.

이어서 실험 2-1, 2, 3, 4의 각가속도를 활용해 I(사각추)값들도 확인해보면 R=0cm, 5cm, 10cm 20cm 로 증가 할수록 I(사각추)값들은 2,095.88 𝑔 ∙ 𝑐𝑚!, 9334.18 𝑔 ∙ 𝑐𝑚!, 31933.76𝑔 ∙ 𝑐𝑚!, 117788.46 𝑔∙𝑐𝑚! 으로점점증가하는것을확인할수있다.이를통해사각추의질량이일정할때회전 반지름을 증가시키면 관성모멘트는 커지는 경향성이 있음을 확인 할 수 있다.

실험 2-1, 2, 3, 4 R=0, 5, 10, 20 일때 오차율들을 비교해보면, 회전 반지름이 0cm 일때의 오차율은 논할 수 없지만 5cm, 10cm, 20cm 로 회전 반지름이 증가 할수록 -34.039%, -14.6428%, - 5.715%로 오차율의 절대값이 점점 감소하는 것을 확인 할 수 있다.

실험 2 의 2, 5에서는 회전 반지름을 R=5cm 로 고정하고, 사각추의 질량 M 을 286.55g 에서 560.09g으로 증가시켜 실험하였다. 이때 각가속도는 0.53 𝑟𝑎𝑑/𝑠!에서 0.511 𝑟𝑎𝑑/𝑠!로 감소하였다. 사각추의 회전 반지름을 고정시키고 질량을 증가시키면 각가속도가 감소하는 것을 확인할 수 있다. 오차율은 사각추 질량 M이 278.55g 일 때 오차율 -34.039%, 사각추 질량 M이 560g일 때 오차율 -0.418%으로 사각추 질량이 증가 할 때 오차율이 작아지는 모습을 확인 할 수 있다.

실험 3 의1, 2는 막대를 회전시킬 때의 축을 달리한 실험이다. 실험 3-1은 회전축을 막대의 중심으로, 실험 3-2는 회전축을 한쪽 끝으로 실험 하였다. 실험 3-1이 실험 3-2 질량 중심이 회전축으로부터 좀 더 가까이 위치하는데 이때 각가속도 평균이 0.622 𝑟𝑎𝑑/𝑠! 에서 0.242 𝑟𝑎𝑑/ 𝑠^2 으로 감소하였고 관성모멘트 𝐼(기본틀 (막대, ./) 값은 205,585.56 𝑔 ∙ 𝑐𝑚^2 에서 528,662.179 𝑔 ∙ 𝑐𝑚!^2 로
증가하였다. 이로 인해 질량 중심이 회전축에 멀어 질수록, 각 가속도 평균이 감소하고
𝐼(기본틀+막대, cm) =𝑚𝑟^2(g/ra −1) 식에 의해 관성 모멘트 값이 증가 함을 확인 할 수 있다. 오차율 %α 또한 은 실험 3-1에서 3-2에서는 -4.872%에서 -22.601%로 절댓값이 증가했으므로 질량 중심이 회전축에 멀어질 수록 오차율의 절댓값이 커짐을 확인 할 수 있다.
[3] 오차 논의 및 검토
우리의 실험은 사각추과 막대를 이용해 관성 모멘트를 구하는 과정에서, 질량 중심에 질량이 집 중해 있다고 가정하고 계산하였다. 하지만 실제로 사각추와 막대의 질량이 질량 중심에 전부 위치하고 있지 않고,부피만큼 분포하고 있기 때문에 관성모멘트의 이론값 𝐼 이론=𝑀𝑅^2 와 (사각추) 실험을 통해 구한 값은 차이가 발생 할 것이다. 각자의 부피에 좀더 적합한 관성모멘트 이론 값 을 도출하고 계산하여 오차율을 줄여보도록 하자.
사각추를 이용해 진행한 실험2의 1, 2, 3, 4, 5의 경우 실제로는 사각추가 직육면체에서 원통 형을 뺀 형상을 하고 있기 때문에 (직육면체의 관성 모멘트) – (원통 모양 구멍의 관성 모멘트)로 계산해야 좀 더 정확한 관성모멘트를 계산할 수 있다. 수식으로 나타내면

식 ᄀ을 활용하여 오차율을 계산하였지만 회전반지름이 바뀌는 실험마다 유의미 하게 오차율이 변화하지 않았다. 이는 실험에 지배적인 영향이 아닌 것을 확인하였다.
막대를 이용한 실험 3의1, 2도 마찬가지로 막대의 밀도가 균일하다고 가정하면 막대의 축이 중심에 있을 때 실험 3-1의 관성모멘트는
1/4𝑀𝑅^2+1/12𝑀𝐿^2 (M:질량,R:질량중심부터의회전반지름,L:막대길이)---ᄂ
한쪽 끝에 있을때 실험 3-2의 관성모멘트는
1/4𝑀𝑅^2+1/3𝑀𝐿^2 (M: 질량,R: 질량 중심 부터의 반지름,L: 막대 길이)--- ᄃ
로 계산 할 수 있다. 이를 활용해 관성모멘트와 오차율을 다시 계산해보면
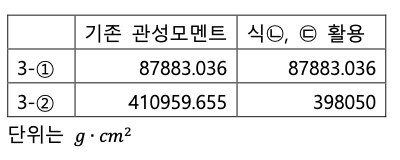

실험 3-1은 막대를 중앙에 두고 돌려서 영향을 크게 끼치지 못했지만 한쪽 끝에다가 놓고 돌린 실험 3-2 는 유의미하게 오차율이 감소한 것을 확인할 수 있다.
[4] 결론
실험 1, 실험 2-1, 2, 3, 4, 5, 실험 3-1, 2에서 각가속도 측정시 표준편차가 0.004, 0.004, 0.00447, 0.00632, 0.00663, 0.003, 0.00748, 0.004 (단위: 𝑟𝑎𝑑/𝑠!)로 상당히 작게 측정되어 신뢰성이 높게 측정되었다고 할 수 있다. 이후의 모든 계산과정에 각가속도를 활용하기 때문에 실험자체의 신뢰성이 높다고 판단 할 수 있다.
실험 2-1의 오차율은 논할 수없고 실험 2-2, 3, 4의 오차율은 -34.0395%, -14.642%, -5.715%로 실험 2-2, 5의 오차율은 -34.039%, -0.418%로 나타났다. 실험 2-2, 3, 4의 비교를 통해 회전 반지름 R 이 커질 수록 각가속도는 감소하고 관성모멘트는 커지고 오차율의 절댓값이 감소하는 것을 확인 할 수 있었다. 실험 2-2, 5의 비교를 통해 질량이 증가 할수록 각가속도는 감소하고, 관성모멘트는 커지는 것을 확인 할 수 있었다. 결과적으로 관성모멘트가 강체의 질량이 커질수록, 회전축으로부터의 거리가 멀어질 수록 커짐으로써 회전시키기 어려워지는 것을 확인할 수 있었다.
실험 3 - 1, 2을 실험하고 -4.872%, -22.601%의 오차율을 계산하였다. 이때 기존의

를 도출하고 활용하면서 오차율을 유의미하게 줄일 수 있었다. 실험 3-1, 2의 관성모멘트 값들을 비교하면서 강체의 관성모멘트가 회전축의 선택에 따라 즉, 회전축에 대한 질량의 분포에 관계함을 확인 할 수 있었다. 전체적으로 회전운동에서의 강체의 관성모멘트는 강체의 질량에만 관계하는 게 아니라, 회전축에 대한 질량의 분포에도 관계함을 이해 할 수 있었다.
'일반물리실험(1)' 카테고리의 다른 글
| [일반물리실험(1)] 8주차 회전 평형(토크의 이해) (0) | 2025.03.23 |
|---|---|
| [일반물리실험(1)] 7주차 탄환의 속도 측정 (0) | 2025.03.22 |
| [일반물리실험(1)] 6주차 구심력 측정 (0) | 2025.03.21 |
| [일반물리실험(1)] 5주차 공기중에서의 소리의 속도 측정 (0) | 2025.03.21 |
| [일반물리실험(1)] 4주차 힘의합성과 분해 (0) | 2025.03.13 |



