[1] 실험값
(1) 용수철저울의 용수철상수(𝑘) 측정
-추걸이의 질량: 5.54 g
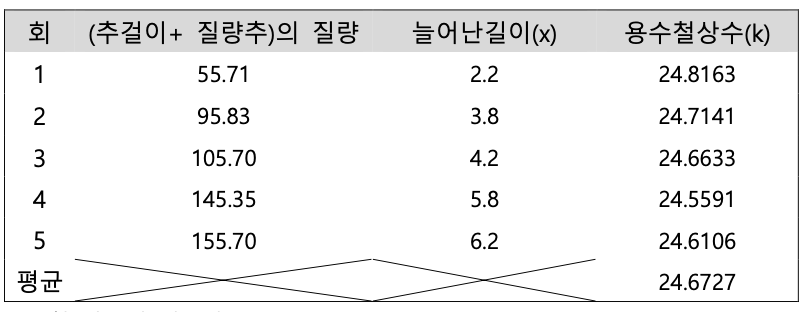
용수철 상수의 평균값: 24.6727N/m
(2) 작용하는 힘의 크기 F만을 변화시켜가며 토크의 크기를 측정
-연결고리의 질량, m=4.72 g
-회전축으로부터 용수철저울과 연결되는 왼쪽 연결고리까지의 거리, 𝑟_s =15.1 cm
-회전축으로부터 추걸이와 연결되는 오른쪽 연결고리까지의 거리, 𝑟_M =14.4 cm


(3) 회전축으로부터 힘의 작용점까지의 거리 𝑟 만을 변화시켜가며 토크의 크기를 측정 𝑀
-(추걸이+질량추)의 질량, M = 155.47 g
(4) 회전축으로부터 힘의 작용점까지 위치벡터 r_M 과 작용한 힘 𝐹가 이루는 각 𝜃만을 변화시켜가며 토크의 크기를 측정
[2] 결과 분석
본 실험은 역학 종합 실험장치에 수평막대를 연직하게 설치하여 회전축에 대해 시계방향으로 돌리는 토크를 용수철저울으로 측정하여 토크의 변수를 알아보는 실험이다. 용수철저울의 탄성계수를 측정하는것을 포함하여 총 4가지의 실험이 이루어졌으며, 2,3,4번 실험은 각각 작용하는 힘의 크기, 회전축으로부터 힘의 작용점까지의 거리, 그리고 회전축으로부터 힘의 작용점까지의 위치 벡터->r_M 와 힘𝐹 가 이루는 각 𝜃를 변화시키며 실험하였다. 모든 실험의 계산값들은 전부 유효숫자를 고려한 값이다.
첫번째 실험 (1)에서는 질량추에 작용하는 중력과 용수철저울의 탄성력이 평형을 이룸을 이용하여 수식 kx=mg, k=mg/x라는 식을 이끌어내어 용수철상수 k의 평균을 구하였고, 1회부터 5회까지 k의 값 은 각각 24.8162 N/m, 24.7141 N/m, 24.6633 N/m, 24.5591 N/m, 24.6106 N/m 이었다. 평균값은 24.6727 N/m 이었으며 표준편차는 0.099 N/m 로 k값들이 일관되게 나온것으로 보아 신뢰할만한 수치 라 생각한다.
두번째 실험(2)에서는, M의 값만 변화시킴으로써 작용하는 힘의 크기와 토크의 관계에 대하여 실 험하였다. M값이 42.00, 71.44, 95.19, 137.78, 155.47일때 측정된 토크는 각각 0.0647 N/m, 0.1057 N/m, 0.1411 N/m, 0.1989 N/m, 0.2268 N/m 이다. 각 M값에 따른 이론적인 토크는 0.0659 N/m, 0.1075 N/m, 0.1410 N/m, 0.2011 N/m, 0.2260 N/m 으로, 각각 오차율 1.8414%, 1.6547%, -0.0697%, 1.1229%, - 0.3182%가 나왔다. 오차율의 이차평균(RMS)은 1.2244%, 표준편차는 0.8849%가 나왔다. F에 따른 토크 의 값을 보여주는 그래프에서, 해당 실험의 데이터들은 F가 증가할 때 토크도 증가하는 경향을 보이며, 추세선 y=0.145x + 0.0048 (R^2=0.9997)을 따르고 있다.
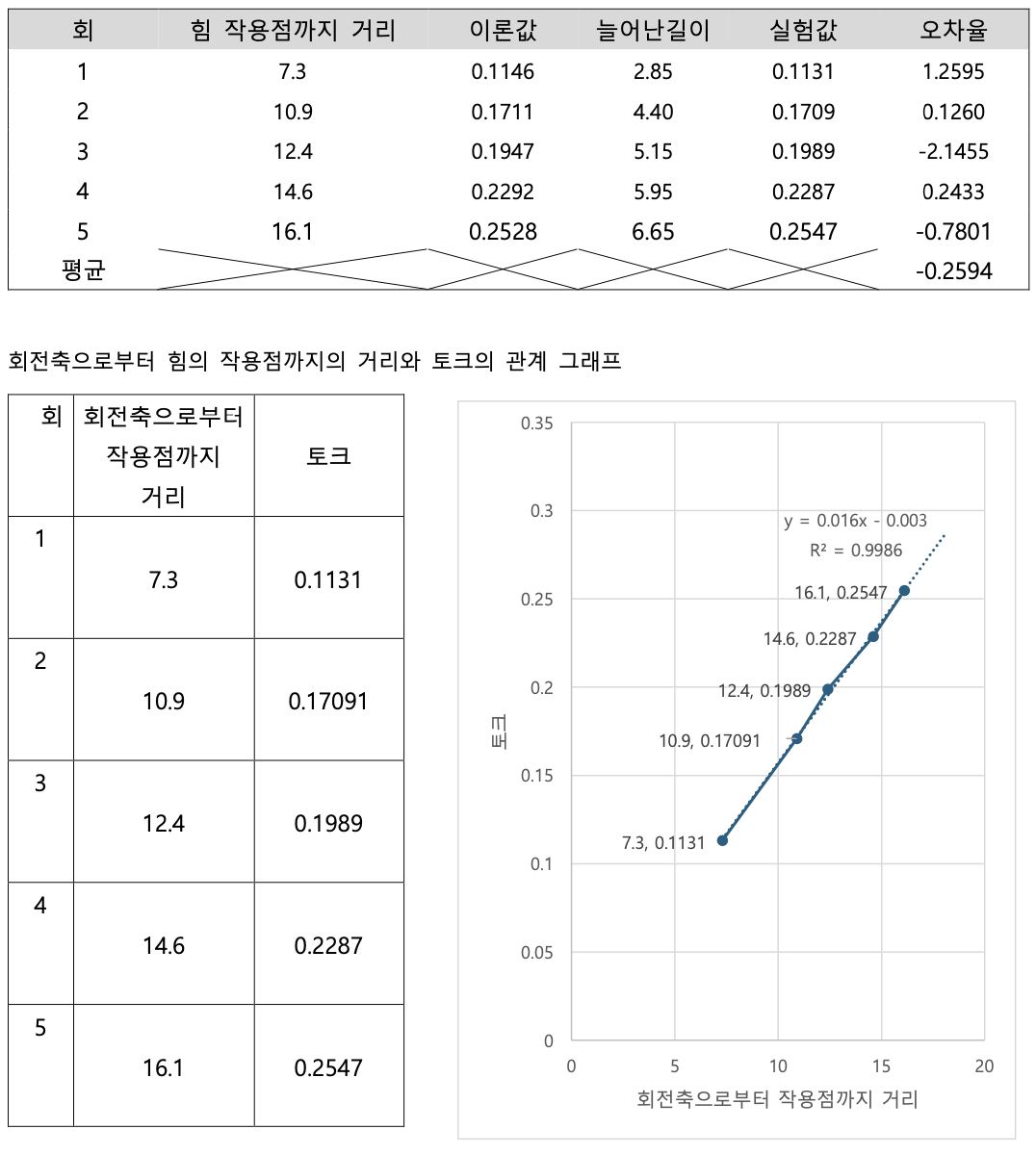
실험(3)은, 회전축으로부터 힘의 작용점까지의 거리 𝑟_M 만을 변화시키며 토크의 크기를 측정하였다. 𝑟_M 이 차례대로 7.3, 10.9, 12.4, 14.6, 16.1일 때 측정된 토크값은 각각 0.1131 N/m, 0.1709 N/m, 0.1989N/m, 0.2287 N/m, 0.2547 N/m 이다. 이론값은 차례대로 0.1146 N/m, 0.1711 N/m, 0.1947 N/m, 0.2292 N/m, 0.2528 N/m 으로 오차율 1.2595%, 0.1260%, -2.1455%, 0.2433%, -0.7801%이다. 이에 대한 이차평균(RMS)은 1.1724%이며 표준편차는 1.1434%이다. 𝑟_M 이 증가함에 따라 토크도 증가하는 경향을 보여주며 추세선 y=0.016x-0.003, R^2 = 0.9986을 따르고 있다.
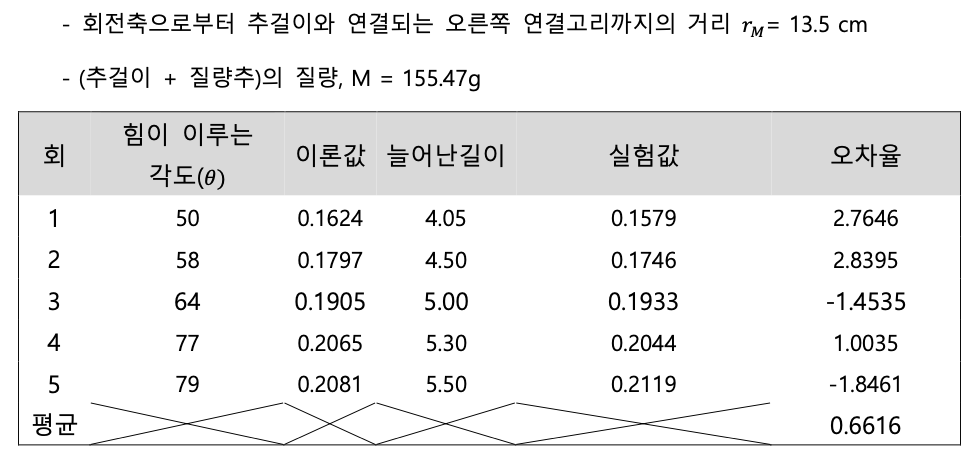
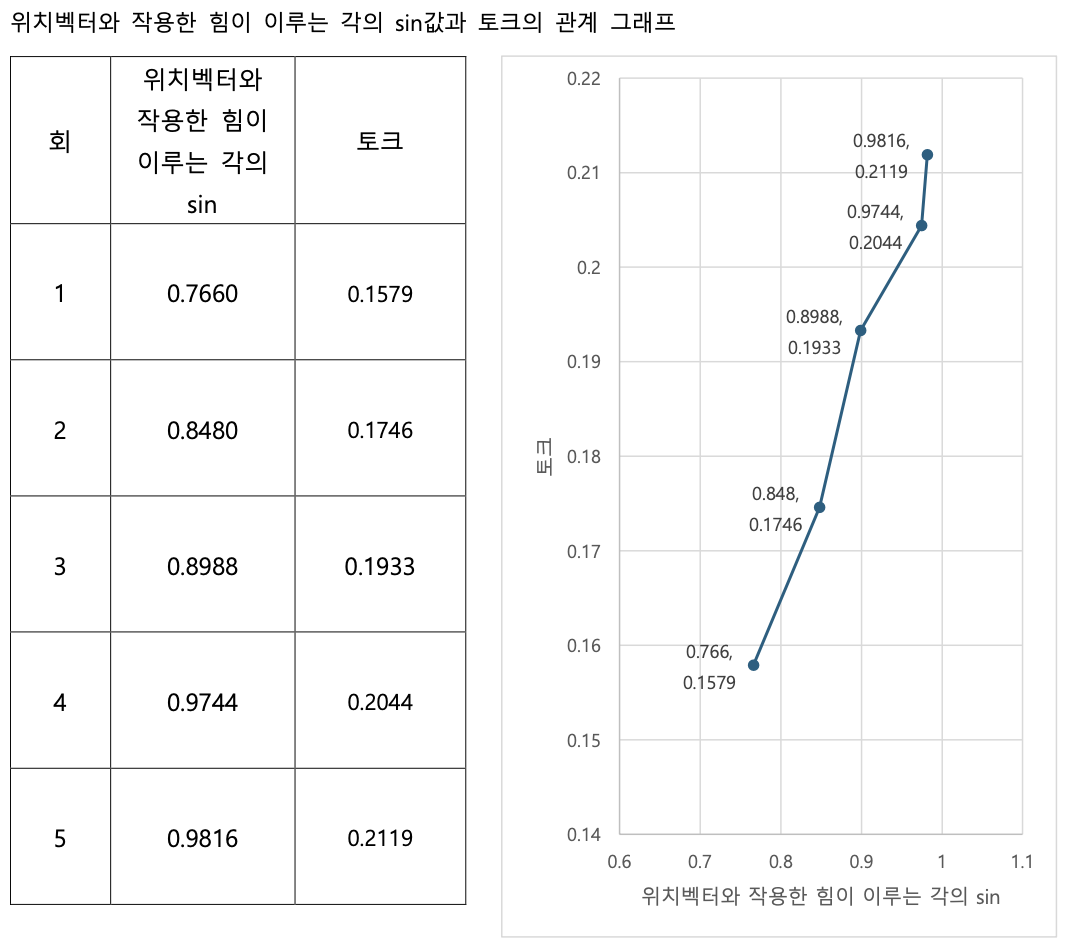
실험(4)는 회전축으로부터 힘의 작용점까지 위치벡터r_M과 힘𝐹가 이루는 각 𝜃를 변화시켜가며 토크의 크기를 측정하였다. 각 𝜃가 50, 58, 64, 77, 79로 변함에 따라 측정된 토크는 0.1579 N/m, 0.1746N/m, 0.1933 N/m, 0.2044 N/m, 0.2119 N/m 이다. 각각 오차율 2.7646%, 2.8395%, -1.4535%, 1.0035%, - 1.8461%로 이차평균(RMS) 2.1087%, 표준편차 2.0022%를 보여준다. 각의 sin값과 토크의 관계를 살펴 보면, sin값이 1에 가까워질수록 토크 또한 커지는 것을 보여준다.
실험 (2),(3),(4)를 통해 작용하는힘(F)이 커질수록, 회전축과 힘의작용점 사이의 거리 𝑟_M 이 커질수록, 위치벡터와 작용한 힘이 이루는 각의 sin값이 커질수록 토크가 커진다는 것을 알 수 있고,𝜏 ∝𝐹sin𝜃라 는 식을 유추해볼 수 있다. 실험(2)의 5번째 측정이 M은 155.47g, 늘어난 길이 5.9cm, 작용점까지의 거 리가 14.4cm이고, 실험(3)의 4번째 측정이 작용점까지의 거리 14.6cm, 늘어난길이 5.95cm, 이고 M이 동일한것을 볼 수 있다. 서로 다른 회차에 이루어진 실험임에도 M이 똑같을 때 늘어난 길이와 작용점 까지의 거리가 거의 비슷하면서도, 실험(3)의 4번째 측정이 작용점까지의 거리와 늘어난 길이 모두 소 폭 커 토크와 작용점까지의 거리가 양의 상관관계를 갖는다는 점을 만족하는것으로 보아 우리 실험의 타당하며 신뢰성 있다고 생각한다.
[3] 오차 논의 및 검토
먼저 길이측정에서 오차가 났다고 생각한다. 회전축으로부터 작용점까지의 길이측정은 자로 진행했 다. 우선 자의 길이 측정이 0.1 (1mm)까지만 가능할 뿐더러, 실험장비 특성상, 자를 공중에 떨어뜨려 재야하므로, 자와 수평막대가 평행하지 않았을 수 있다. 최대한 평행을 맞추려 했지만, 사람이 눈으로 하므로, 어쩔 수 없이 오차가 발생할 수밖에 없다. 자가 흔들리는 각도와 시선의 오차를 포함하여 최대 +-3도로 생각할때, 길이 13.5cm 기준으로 +-0.02cm가량의 오차가 발생하게 된다. 또한 손떨림 및 시 점차이로 인한 오차를 집에서 간략하게 재현해본 결과 대략 +-0.3cm까지 차이가 날 수 있는 것을 보 았다. 이를 실험(3)에 적용하여보면, 3회측정에서 기존의 측정값인 거리 12.4cm에 대한 오차율이 -2.1455%에서 0.2674%까지 줄어드는 것을 확인할 수 있다.
또 실험(4)의 평균적인 오차율이 가장 크게 나타나는데, 이에 대한 이유로는, 회전축의 마찰력과 각 도측정에서 찾을 수 있다고 생각한다. 실험(4)에서는, 정밀하게 측정하기 위해 추를 먼저 세팅해두고, 용수철 저울과 역학종합 실험장치 사이에 얇은 물체를 집어넣어 용수철 저울을 최대한 세밀하게 움직 일 수 있도록 하였다. 이 과정에서, 용수철 저울의 측정값은 눈금이 바뀔정도로 변하지만, 수평막대는 움직임을 관찰할 수 없는 경우를 목격할 수 있었다. 이 때문에 오차가 발생하였을것이라 생각한다. 실 제로 실험(4)에서 늘어난 길이를 +-0.1cm씩 조정할 경우, 오차율이 0.4699%, 0.7667%, 0.5022%, - 0.8006%, -0.0554%까지 줄어드는 것을 확인할 수 있다.
[4] 결론
역학종합 실험장치를 통해 토크에 영향을 주는 요소들을 알아보았다. 실험결과를 토대로 토크가 회전 축으로부터 힘의 작용점까지의 거리와 작용한 힘의 크기에 비례하고, 힘이 막대에 수직하게 작용할수 록 크다는 점을 𝜏 ∝𝐹sin𝜃라는 식으로 표현할 수 있었다. 만약 힘의 작용점을 눈금으로 표시하고, 분 해하여 길이를 잰 후 다시 조립하여 더욱 정확하게 측정하거나, 회전축에 윤활유를 발라 마찰력을 줄 이는 방법 등을 사용하면 오차율을 더 줄일 수 있을 것이다.
'일반물리실험(1)' 카테고리의 다른 글
| [일반물리실험(1)] 7주차 탄환의 속도 측정 (0) | 2025.03.22 |
|---|---|
| [일반물리실험(1)] 6주차 구심력 측정 (0) | 2025.03.21 |
| [일반물리실험(1)] 5주차 공기중에서의 소리의 속도 측정 (0) | 2025.03.21 |
| [일반물리실험(1)] 4주차 힘의합성과 분해 (0) | 2025.03.13 |
| [일반물리실험(1)] 3주차 글라이더의 가속도 측정 (0) | 2025.03.13 |



