

[1] 실험값
[2] 결과 분석
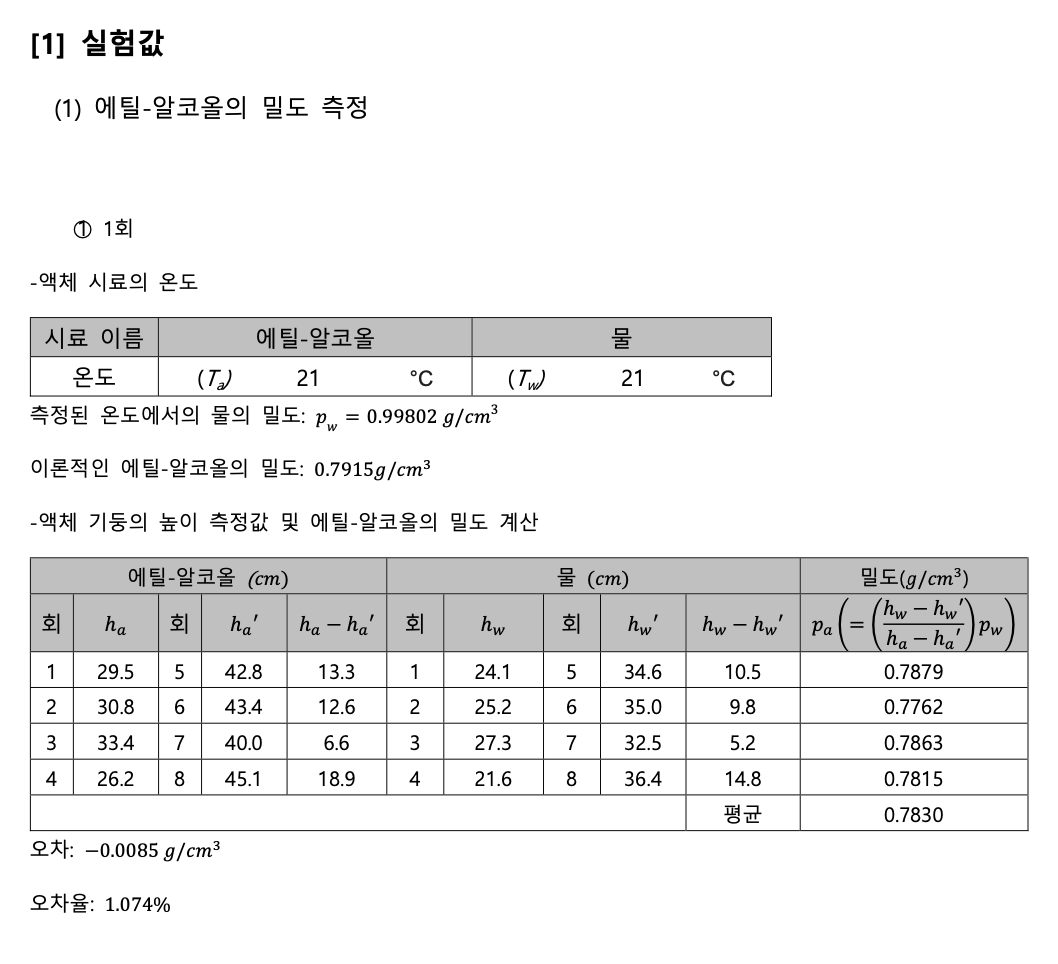
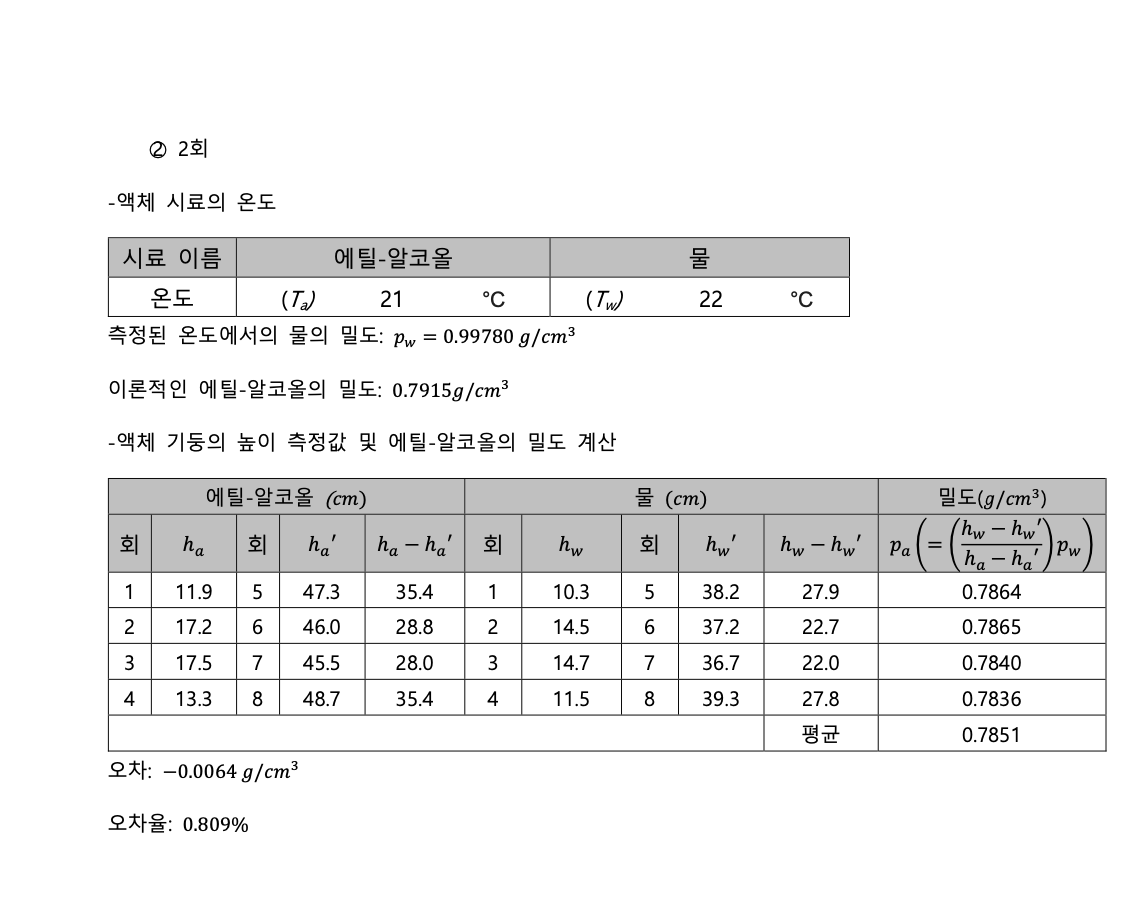
첫번째 에탄올 실험에서는 평균 밀도 0.7830𝑔/𝑐𝑚^3, 표준편차 0.005𝑔/𝑐𝑚^3오차율 1.074%가 나왔 고, 두번째 에탄올 실험에서는 평균밀도 0.7851𝑔/𝑐𝑚^3, 표준편차 0.002𝑔/𝑐𝑚^3 오차율 0.809%가 나 왔다. 전체적인 실험 데이터를 보면 2번째 에탄올 실험에서 액체 기둥의 높이 변화 값이 대체로 크고, 오차율과 표준편차가 전체적으로 더 작은 것을 알 수 있다.
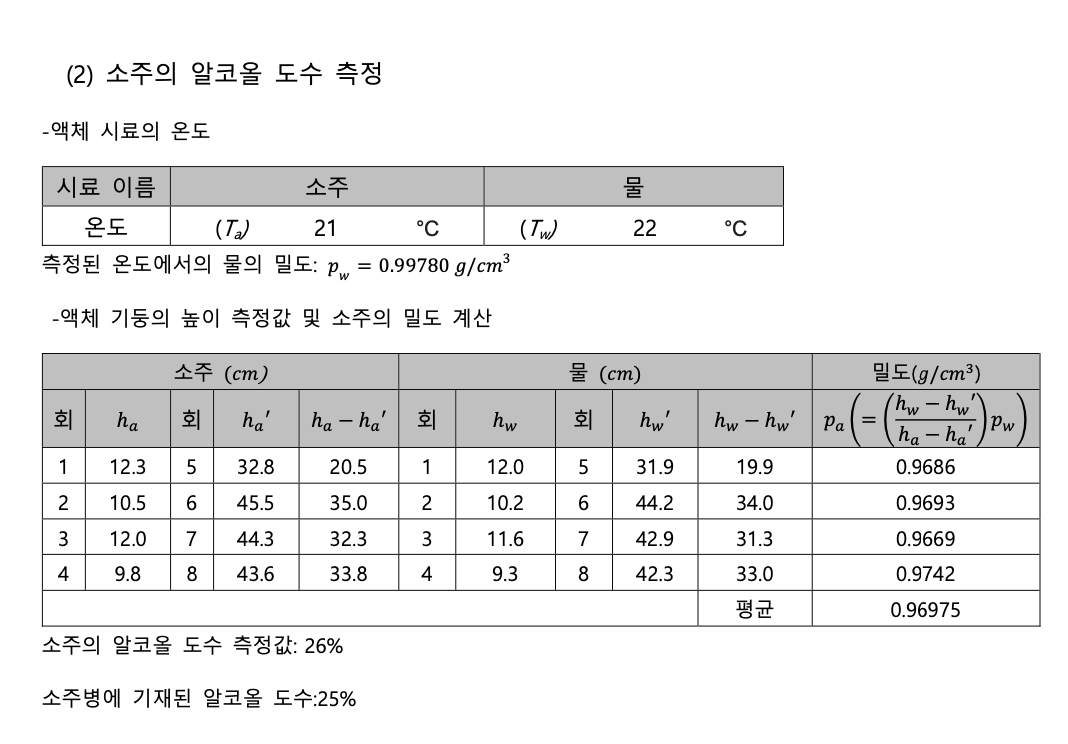
소주에 대한 실험에서는, 3회까지의 측정에서 표준편차가 0.001𝑔/𝑐𝑚^3이지만, 4회까지의 측정에선 표준편차가 0.003𝑔/𝑐𝑚^3으로 이전까지의 측정에 비해 다소 증가하였다. 평균밀도는0.96976𝑔/𝑐𝑚^3 으로, 교재에 주어진 이론표에 의하면, 대략 도수 26도에 가까운 결과이다.
[3] 오차 논의 및 검토
실험장치에서 액체의 높이를 측정할 때, 소수점 2번째 자리까지는 정확히 측정하는 것이 어렵다. 반올림을 하였다고 가정했을 때 측정된 높이의 범위는 측정값 ±0.05𝑐𝑚이므로, 높이차는 계산값 ±0.1𝑐𝑚 까지 오차가 발생할 수 있다. 밀도를 구하는 과정에서, 두 액체기둥의 높이 변화량의 비 율을 구하는데, 이때 절대적인 수치가 클수록, 오차범위의 상대적인 비율이 작아지므로, 전체적인 높이 변화량을 크게 설정했던 에탄올 측정 2번째 실험에서의 결과가 1번째 실험에 비해 평균적으 로 오차와 표준편차가 작게 나타나는 점을 설명할 수 있다.
소주에 대한 실험에서, 소주에 대한 밀도를 통해 소주의 도수를 구한 결과 26도로 이론 값인 25 도에 비해 높게 나왔다. 이에 대한 이유로는, 주어진 이론표는 소주의 온도가 15도 기준이지만, 실험은 소주온도 21도에서 진행되었다. 액체는 열팽창에 의해 온도가 높을 때 밀도가 낮아지고, 온도가 낮을 때 밀도가 상대적으로 높으므로, 이러한 이유에서 실제 도수보다 도수가 높게 분석 되었을 것이다.
소주에 대한 실험 4번째 측정에서, 이전의 수치들에 비해 편차가 큰 값이 측정되었는데, 측정높이 의 오차범위를 생각하여 소주의 높이 변화량을33.7~33.9𝑐𝑚, 물의 높이 변화량을 32.9~33.1𝑐𝑚로 계산했을 때, 밀도는 0.9800~0.9684𝑔/𝑐𝑚^3의 범위로 계산된다. 이전까지의 평균값인 0.9683𝑔/𝑐𝑚^3 이 해당 범위 안에 들어가는 것 보아 4회째의 측정에서 눈금측정 관련하여 눈금의 최소단위인 0.1𝑐𝑚보다 작은 수준에서의 오차가 발생하여 편차가 늘었다고 볼 수 있다.
[4] 결론
우리의 실험은, 에탄올 밀도측정에서는 매 측정값이 이론 값보다 일관되게 낮고, 표준편차는 각각 0.005𝑔/𝑐𝑚^3, 0.002𝑔/𝑐𝑚^3인 점, 오차율은 각각 1.074%, 0.809%인 점과 높이차를 크게 설정하였을 때 평균적으로 일관되게 신뢰성과 타당성이 높아지는 것을 보아 믿을 수 있는 실험이라고 할 수 있다. 또한 비록 소주의 알코올 도수 측정실험의 마지막 4회 측정값이 이전의 데이터들에 비해 편차가 크지만, 그 이전까지 데이터들의 표준편차가 0.001𝑔/𝑐𝑚^3이고, 4회를 포함해도 0.003𝑔/𝑐𝑚^3 으로 에탄올 밀도측정실험의 표준편차를 생각했을 때 신뢰할만한 실험이라 할 수 있다.
섭씨 21도의 실험데이터를 섭씨15도일때의 이론데이터로 해석하여 소주의 도수가 이론 값보다 소폭 높게 나온 것을 감안하였을 때, 우리는 소주의 도수를 거의 정확하게 측정할 수 있었고, 이 를 통해 Hare의 장치를 이용한 소주의 밀도 측정값이 타당한 결과였다는 것을 알 수 있다.
Hare의 장치를 통해 실험을 진행하며 정적평형 상태에 놓인 유체에 작용하는 알짜 힘이 0일수밖 일 없다는 것을 통해 뉴턴의 제1법칙을 이해할 수 있었다.
'일반물리실험(1)' 카테고리의 다른 글
| [일반물리실험(1)] 6주차 구심력 측정 (0) | 2025.03.21 |
|---|---|
| [일반물리실험(1)] 5주차 공기중에서의 소리의 속도 측정 (0) | 2025.03.21 |
| [일반물리실험(1)] 4주차 힘의합성과 분해 (0) | 2025.03.13 |
| [일반물리실험(1)] 3주차 글라이더의 가속도 측정 (0) | 2025.03.13 |
| [일반물리실험(1)] 2주차 선팽창계수 측정 (0) | 2025.03.10 |



